Sine waves are simple things and provide a nice entry point to learning audio signal processing. So far we've been able to discuss things like frequency and amplitude using nothing but individual sine wave oscillators.
But the thing is, a solitary sine wave is not very interesting to listen to. It's a blank slate, devoid of any color, character, or drama.
Things start to get much more interesting when we have multiple sine wave oscillators at our disposal. What we can do is combine them to produce more complex sound waves. This technique is called additive synthesis.
This post is part of a series I'm writing about making sounds and music with the Web Audio API. It is written for JavaScript developers who don't necessarily have any background in music or audio engineering.
- Part 0: What Is the Web Audio API?
- Part 1: Signals and Sine Waves
- Part 2: Controlling Frequency and Pitch
- Part 3: Controlling Amplitude and Loudness
- Part 4: Additive Synthesis And the Harmonic Series
What Happens When I Combine Two Or More Sine Waves?
As we discussed in Part 1, a digital sound signal is essentially just a (very large) array of individual numbers that represent the sound's amplitude over time.
When we want to combine two sound signals together, all we have to do is add the samples from both signals together for each time step.
// Pseudocode
for (let i = 0 ; i < signal1.length ; i++) {
combo[i] = signal1[i] + signal2[i];
}
What we end up with when we do this is a third sound signal that represents the combination of the originals. For two sine wave inputs, we get something that no longer looks like a sine wave:
We have just synthesized a wave using additive synthesis.
When we combine signals like this, some samples end up having a higher amplitude than in either of the originals, which makes sense because what we're doing is adding signals together. But some samples are lower than either of the originals, which is because sine waves also oscillate to the negative side of the x-axis, and we end up effectively subtracting samples.
The extreme form of this kind of subtraction is with two waves that are exactly opposite of each other: Waves that have the same frequency and amplitude, but are in opposite phases. They completely cancel each other out, leaving nothing but silence.
This is what happens in noise-canceling headphones. They synthesize sound waves in real time that are the exact opposite of the environmental noise reaching your ears. The goal is that you end up hearing none of that noise because the sounds cancel each other out.
When we want to do additive synthesis in Web Audio, we luckily don't actually need to sum up any numbers manually. The API allows connecting two or more source nodes to the same destination. When this happens, it does the addition for every sample automatically behind the scenes. So for example, we can spin up three OscillatorNodes, start them at the same time, and connect them to the destination. What we hear is the combination wave synthesized from those three oscillators.
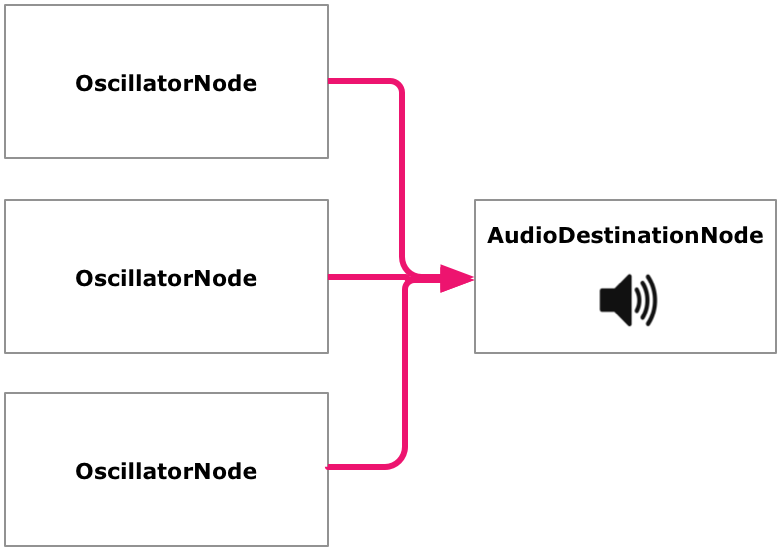
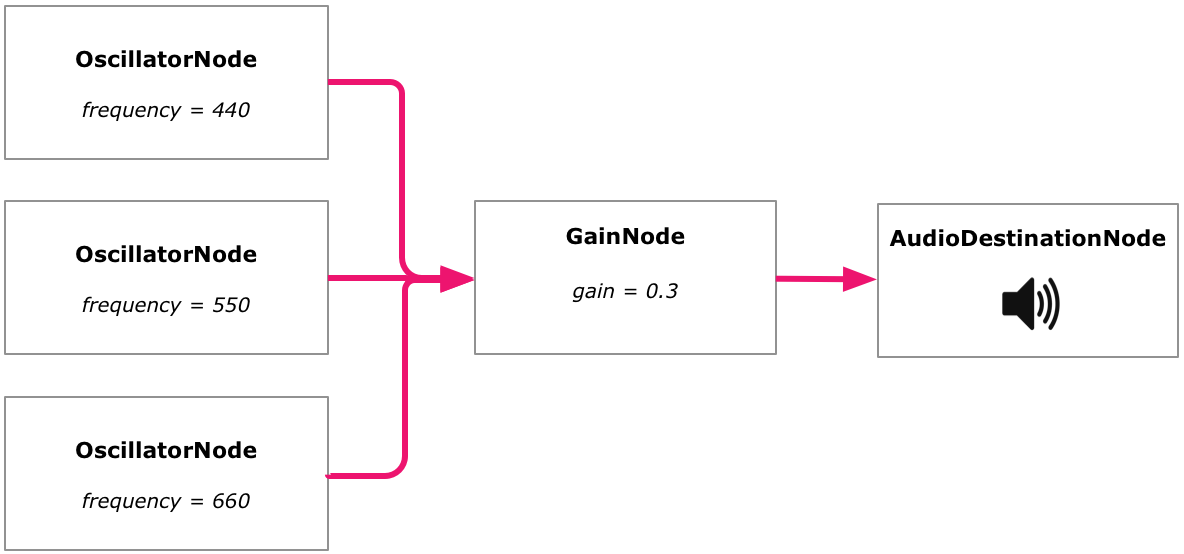
Usually we also want to have at least one gain involved though. That's because when we are adding individual signals that are in the [-1, 1] range, we very quickly get combined signals that don't fit in that range, and we have seen how that may cause clipping to occur. We can use a gain to multiply the combined signal with some constant number (like 0.5) to scale it back down.
Here's an example that uses three oscillators to make an approximate major triad chord above the A4 note, and a gain to scale it down.
let audioCtx = new AudioContext(); Run / Edit
let osc1 = audioCtx.createOscillator();
let osc2 = audioCtx.createOscillator();
let osc3 = audioCtx.createOscillator();
let masterGain = audioCtx.createGain();
osc1.frequency.value = 440;
osc2.frequency.value = 550;
osc3.frequency.value = 660;
masterGain.gain.value = 0.3;
osc1.connect(masterGain);
osc2.connect(masterGain);
osc3.connect(masterGain);
masterGain.connect(audioCtx.destination);
osc1.start();
osc2.start();
osc3.start();
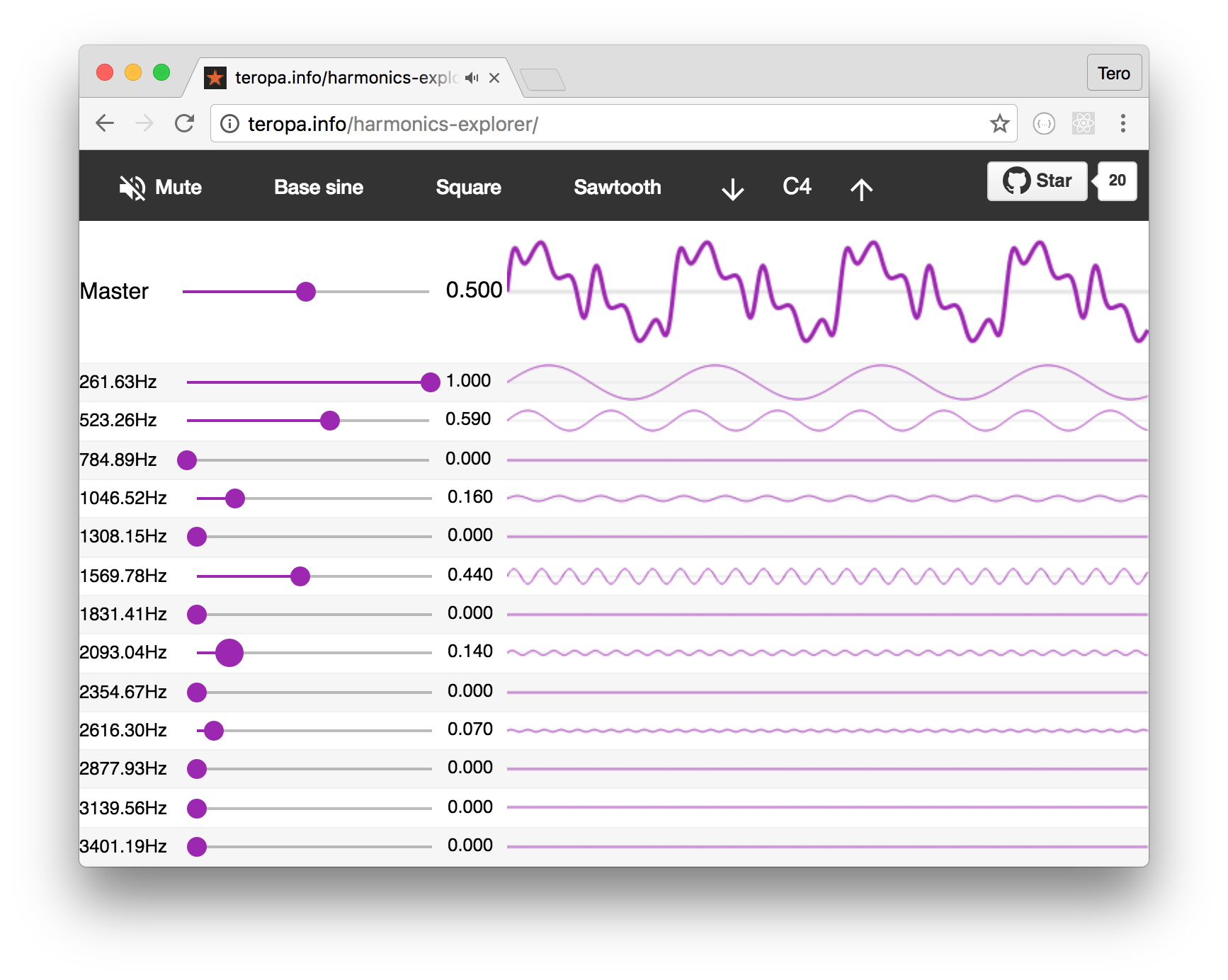
What Is The Harmonic Series?
We just combined three sine waves with three different frequencies to produce a musical major triad. Of course, this is just one of an infinite amount of frequency combinations we could have used. How can we navigate this infinite frequency space to find interesting sounds?
Well, one way to do it is to pick one frequency - any frequency - and then produce integer multiples of that frequency. For example, starting from 440Hz we get the following series:
440Hz2 * 440Hz = 880Hz3 * 440Hz = 1320Hz4 * 440Hz = 1760Hz5 * 440Hz = 2200Hz6 * 440Hz = 2640Hz- ...
This is called a harmonic series. We can mount such a series on any fundamental frequency (like 440Hz). Then we add integer multiples to it, called harmonics or overtones (880Hz, 1320Hz...).
The reason why this relationship between frequencies is special is that it occurs naturally in the physical world. For example, when we pluck the string of a guitar or a violin, it vibrates on a certain frequency determined by the string length (L), but at the same time it also vibrates also on a number of higher frequencies, which happen to be based on integer divisions of the original string length: L/2, L/3, L/4...
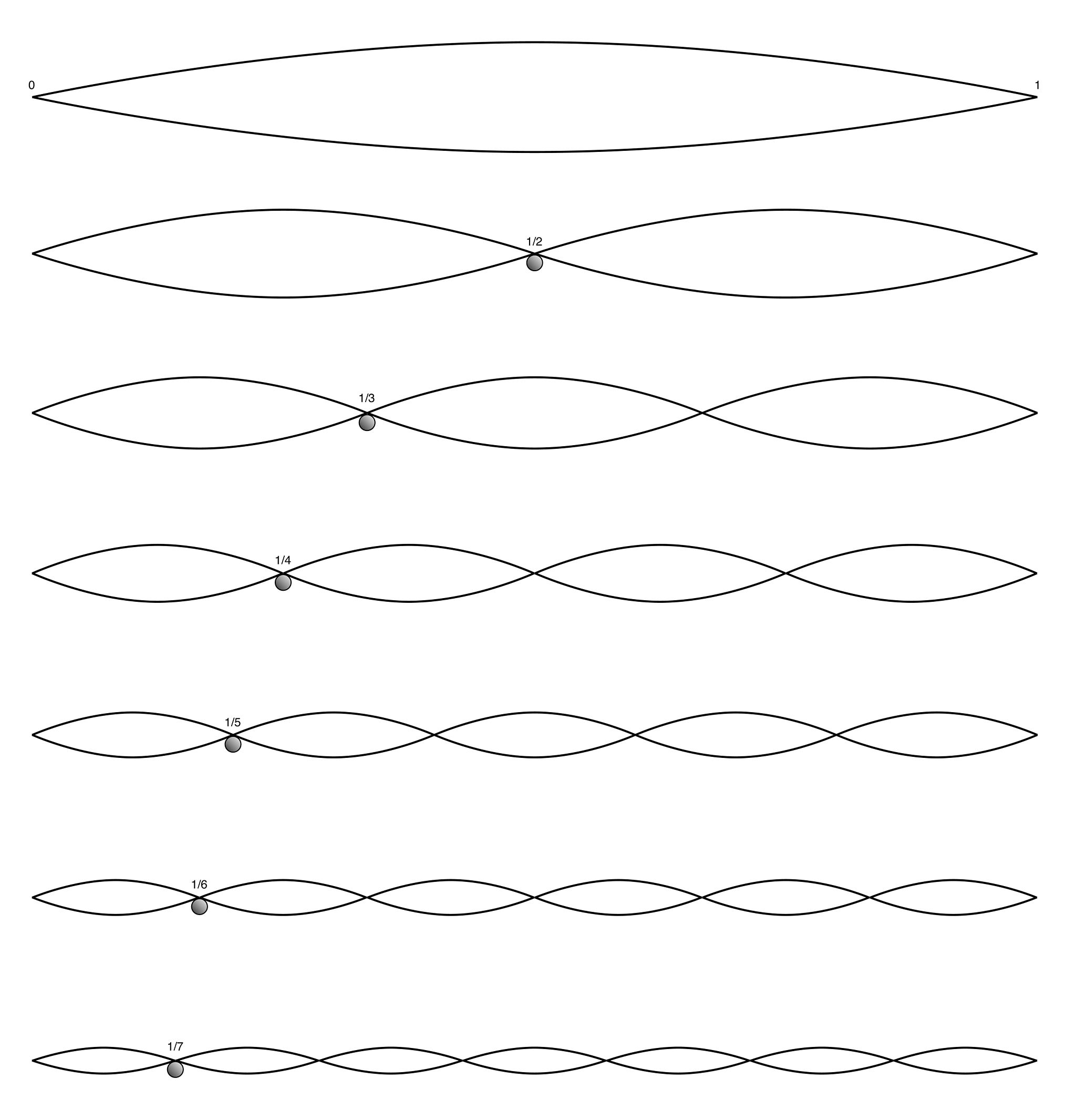 So when you pluck a string instrument, you're not generating a sine wave or any purely single-frequency sound. You're producing a combination of sounds across these different frequencies – a harmonic overtone series. The same is true for all natural sounds out there in the world.
So when you pluck a string instrument, you're not generating a sine wave or any purely single-frequency sound. You're producing a combination of sounds across these different frequencies – a harmonic overtone series. The same is true for all natural sounds out there in the world.
Here's a beautiful interactive visualization by Alexander Chen, with which you can listen to the harmonic series.
Real-world sounds don't only vibrate at exact harmonic intervals though. Any naturally occurring sound also demonstrates a degree of inharmonicity, or presence of overtones elsewhere on the spectrum than in the exact harmonic series. It is the combination of harmonic and inharmonic frequencies and their relationships over time that gives each sound its individual character.
Now, the relationships between frequencies in the harmonic series are not only natural, but also inherently musical, and that is to do with how they produce musical intervals.
As we have discussed, there's an exponential relationship between frequencies and musical pitches. When we get higher on the frequency spectrum, the same absolute distance in frequency spans a much smaller space in musical notes than on the lower ends. Since the distance between every two frequencies in a harmonic series is constant (equal to the fundamental frequency), the musical intervals between consecutive harmonics get smaller and smaller the higher we get.
What every harmonic series in fact includes at its base is a set of diminishing musical intervals:
These are the most fundamental intervals in western music. They were famously used by Richard Strauss in the opening "Sunrise" fanfare of "Also Sprach Zarathustra". The intervals between the first four notes are a perfect fifth, a perfect fourth, and a major third.
How Can I Synthesize Sounds Using The Harmonic Series?
We can use the above technique of combining sine waves to put together a number of harmonics from the harmonic series. Here's a combination of four waves - a fundamental and three of its harmonics from the series that we just visualized:
What's really interesting about this is is that, unlike with the major triad we made earlier, this time you don't actually hear three different sounds. You only hear the lowest one, A4, but it no longer sounds like just a sine wave!
What's happening in your brain is something called "fusion". Your auditory system combines harmonically related signals so that it sounds like all you're hearing is the fundamental frequency. The harmonics only serve to add "color" to the sound, changing its timbre.
This is the key idea behind additive synthesis. By combining different harmonics (as well as non-harmonic frequencies) and varying their relationships over time, we can produce different kinds of sounds.
Actually, this idea doesn't only apply to synthesis but to all sound. When you play the same note on a guitar and a piano, you're hearing the same base frequency, but very different sounds. The difference is caused by the difference in the overtone structures between these instruments.
Theoretically we could also synthesize a guitar or a piano using nothing but sine waves, by creating the exact same wave structure that they produce. In practice, this is easier said than done because of the enormous complexity of those sounds and the ways they evolve over time.
Here's how we can produce this particular timbre in Web Audio:
let audioCtx = new AudioContext(); Run / Edit
let fundamental = audioCtx.createOscillator();
let overtone1 = audioCtx.createOscillator();
let overtone2 = audioCtx.createOscillator();
let overtone3 = audioCtx.createOscillator();
let overtone1Gain = audioCtx.createGain();
let overtone2Gain = audioCtx.createGain();
let overtone3Gain = audioCtx.createGain();
let masterGain = audioCtx.createGain();
fundamental.frequency.value = 440;
overtone1.frequency.value = 880;
overtone2.frequency.value = 1320;
overtone3.frequency.value = 1760;
overtone1Gain.gain.value = 0.1;
overtone2Gain.gain.value = 0.2;
overtone3Gain.gain.value = 0.5
masterGain.gain.value = 0.3;
fundamental.connect(masterGain);
overtone1.connect(overtone1Gain);
overtone2.connect(overtone2Gain);
overtone3.connect(overtone3Gain);
overtone1Gain.connect(masterGain);
overtone2Gain.connect(masterGain);
overtone3Gain.connect(masterGain);
masterGain.connect(audioCtx.destination);
fundamental.start(0);
overtone1.start(0);
overtone2.start(0);
overtone3.start(0);
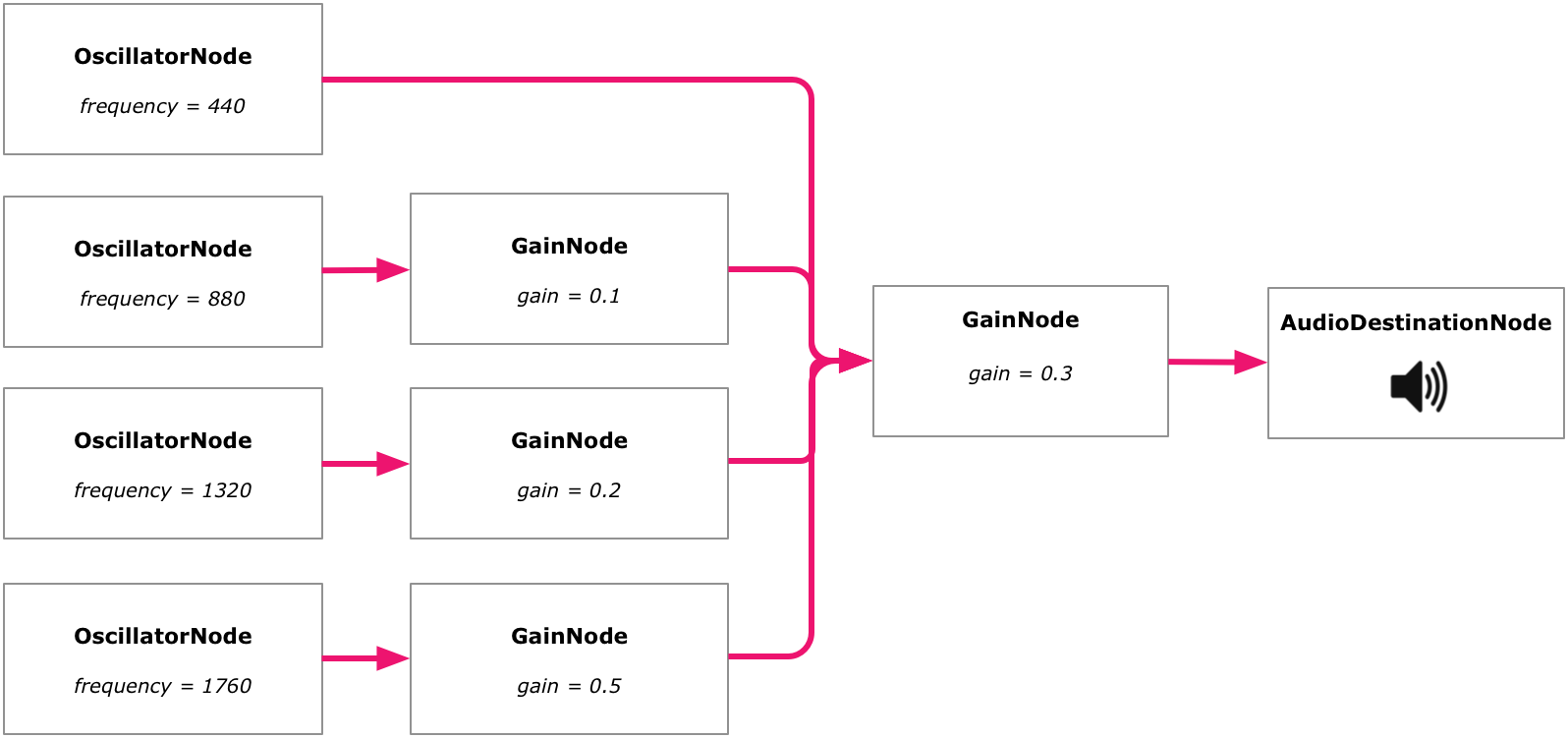
In addition to the oscillators we saw earlier, this time we're also using individual gains, one for each frequency. We want to mix in different harmonic partials with different amplitude relationships to get the sound we want. In this case, we're using the full amplitude for the fundamental, and then 0.1, 0.2, and 0.5 for the harmonics, respectively.
We can package this all up into an ES2015 class so that we have a "synth" we can use to play any musical notes, similarly to what we did using plain sine waves earlier. We can play notes on any frequencies, and as long as the relationship between the partials stay the same, we'll maintain the same timbre for our "instrument":
let audioCtx = new AudioContext(); Run / Edit
class HarmonicSynth {
/**
* Given an array of overtone amplitudes, construct an additive
* synth for that overtone structure
*/
constructor(partialAmplitudes) {
this.partials = partialAmplitudes
.map(() => audioCtx.createOscillator());
this.partialGains = partialAmplitudes
.map(() => audioCtx.createGain());
this.masterGain = audioCtx.createGain();
partialAmplitudes.forEach((amp, index) => {
this.partialGains[index].gain.value = amp;
this.partials[index].connect(this.partialGains[index]);
this.partialGains[index].connect(this.masterGain);
});
this.masterGain.gain.value = 1 / partialAmplitudes.length;
}
connect(dest) {
this.masterGain.connect(dest);
}
disconnect() {
this.masterGain.disconnect();
}
start(time = 0) {
this.partials.forEach(o => o.start(time));
}
stop(time = 0) {
this.partials.forEach(o => o.stop(time));
}
setFrequencyAtTime(frequency, time) {
this.partials.forEach((o, index) => {
o.frequency.setValueAtTime(frequency * (index + 1), time);
});
}
exponentialRampToFrequencyAtTime(frequency, time) {
this.partials.forEach((o, index) => {
o.frequency.exponentialRampToValueAtTime(frequency * (index + 1), time);
});
}
}
const G4 = 440 * Math.pow(2, -2/12);
const A4 = 440;
const F4 = 440 * Math.pow(2, -4/12);
const F3 = 440 * Math.pow(2, -16/12);
const C4 = 440 * Math.pow(2, -9/12);
let synth = new HarmonicSynth([1, 0.1, 0.2, 0.5]);
let t = audioCtx.currentTime;
synth.setFrequencyAtTime(G4, t);
synth.setFrequencyAtTime(G4, t + 0.95);
synth.exponentialRampToFrequencyAtTime(A4, t + 1);
synth.setFrequencyAtTime(A4, t + 1.95);
synth.exponentialRampToFrequencyAtTime(F4, t + 2);
synth.setFrequencyAtTime(F4, t + 2.95);
synth.exponentialRampToFrequencyAtTime(F3, t + 3);
synth.setFrequencyAtTime(F3, t + 3.95);
synth.exponentialRampToFrequencyAtTime(C4, t + 4);
synth.connect(audioCtx.destination);
synth.start();
synth.stop(audioCtx.currentTime + 6);
In musical programming environments people often talk about patches, which are basically preconfigured combinations of simpler audio primitives such as oscillators and gains with particular parameters. Combining them into patches allows for easier reuse.
With Web Audio we can do the same using the general purpose abstraction mechanisms available to us in the JavaScript language, as we have done here with the HarmonicSynth class.
There's a vast space of timbres one can generate from the harmonic series, and you can now easily explore it by constructing HarmonicSynths with different overtone structures. Here are a couple of more interesting examples.
We can produce a sawtooth wave ( ) by oscillating on every frequency of the harmonic series, with amplitudes that decrease as the frequencies increase: The first harmonic has an amplitude of
) by oscillating on every frequency of the harmonic series, with amplitudes that decrease as the frequencies increase: The first harmonic has an amplitude of 1/2 of the fundamental, the second has 1/3 and so on:
let partials = []; Run / Edit
for (let i=1 ; i <= 45 ; i++) {
partials.push(1 / i);
}
let synth = new HarmonicSynth(partials);
synth.setFrequencyAtTime(440, audioCtx.currentTime);
synth.connect(audioCtx.destination);
synth.start(0);
Here, we are using a bank of 45 oscillators. In theory, there's an infinite amount of harmonics in the harmonic series and you would need all of them to make a perfect sawtooth shape. But when making sounds we only need to go up to the upper reaches of human hearing, which, as we discussed earlier, is no more than 20kHZ.
In digital audio we also have a practical hard limit caused by our 44.1kHz sample rate. With this sample rate we can only represent sounds at a frequency of half of that, 22.05kHz.
If we go and eliminate all the even harmonics from our sawtooth wave, we end up with a square wave ( ) with yet another kind of timbre:
) with yet another kind of timbre:
let partials = []; Run / Edit
for (let i=1 ; i <= 45 ; i++) {
if (i % 2 !== 0) {
partials.push(1 / i);
}
}
let synth = new HarmonicSynth(partials);
synth.setFrequencyAtTime(440, audioCtx.currentTime);
synth.connect(audioCtx.destination);
synth.start(0);
You usually wouldn't bother setting up an OscillatorNode bank just to make a sawtooth or a square wave. That's because these waveshapes are natively supported in Web Audio and you can make them by setting the type of a single oscillator. But it's interesting to see how they relate to sine waves and how we can reproduce them this way.
We also saw another way to make a square wave earlier, when we were discussing amplitude control. When we overdrove a sine wave's amplitude so that its peaks were clipped off, the resulting waveshape was a square wave.
I've made a little interactive application you can use to further explore the harmonic series, or at least the first 12 harmonics in it:
Beating
We've barely scratched the surface of what we can do with additive synthesis, and to conclude we're going to discuss one more interesting technique, which is to combine sound waves that have almost but not quite the same frequency. The interference pattern between the waves changes gradually over time as they fall in and out of phase:
This effect is called beating. It is a result of the gradually changing wave phases shifting between reinforcing each other and canceling each other. The resulting effect is pretty remarkable, and we can hear it by setting up oscillators that have nearly the same frequency. For example, using frequencies 330 and 330.2 we get a sound that comes and goes every few seconds:
let audioCtx = new AudioContext(); Run / Edit
let osc1 = audioCtx.createOscillator();
let osc2 = audioCtx.createOscillator();
let gain = audioCtx.createGain();
osc1.frequency.value = 330;
osc2.frequency.value = 330.2;
gain.gain.value = 0.5;
osc1.connect(gain);
osc2.connect(gain);
gain.connect(audioCtx.destination);
osc1.start();
osc2.start();
osc1.stop(audioCtx.currentTime + 20);
osc2.stop(audioCtx.currentTime + 20);
By combining several of these beating pairs together, we get more and more interesting patterns: Different beating intervals make different pairs come and go at different speeds, resulting in seemingly complex changes over time. There are shifts not only in timbre, but also in the perceived pitch of the sound:
let audioCtx = new AudioContext(); Run / Edit
let osc1 = audioCtx.createOscillator();
let osc2 = audioCtx.createOscillator();
let gain1 = audioCtx.createGain();
let osc3 = audioCtx.createOscillator();
let osc4 = audioCtx.createOscillator();
let gain2 = audioCtx.createGain();
let osc5 = audioCtx.createOscillator();
let osc6 = audioCtx.createOscillator();
let gain3 = audioCtx.createGain();
let masterGain = audioCtx.createGain();
osc1.frequency.value = 330;
osc2.frequency.value = 330.2;
gain1.gain.value = 0.5;
osc3.frequency.value = 440;
osc4.frequency.value = 440.33;
gain2.gain.value = 0.5;
osc5.frequency.value = 587;
osc6.frequency.value = 587.25;
gain3.gain.value = 0.5;
masterGain.gain.value = 0.5;
osc1.connect(gain1);
osc2.connect(gain1);
gain1.connect(masterGain);
osc3.connect(gain2);
osc4.connect(gain2);
gain2.connect(masterGain);
osc5.connect(gain3);
osc6.connect(gain3);
gain3.connect(masterGain);
masterGain.connect(audioCtx.destination);
osc1.start();
osc2.start();
osc3.start();
osc4.start();
osc5.start();
osc6.start();
Tero Parviainen is an independent software developer and writer.
Tero is the author of two books: Build Your Own AngularJS and Real Time Web Application development using Vert.x 2.0. He also likes to write in-depth articles on his blog, some examples of this being The Full-Stack Redux Tutorial and JavaScript Systems Music.